Dualidades
Entre los poliedros regulares se establecen relaciones duales, por parejas.
Entre los poliedros regulares se establecen relaciones duales, por parejas. De estas relaciones, unas son muy sencillas, otras hay más complejas, pero en definitiva todas responden al hecho de que los poliedros regulares no constituyen una serie de cinco cuerpos geométricos aislados, individuales y estáticos, en realidad, deben ser estudiados como un conjunto dinámico que permita comprobar mejor la generación particular de cada uno de ellos por evoluciones y relaciones de y entre los demás poliedros.
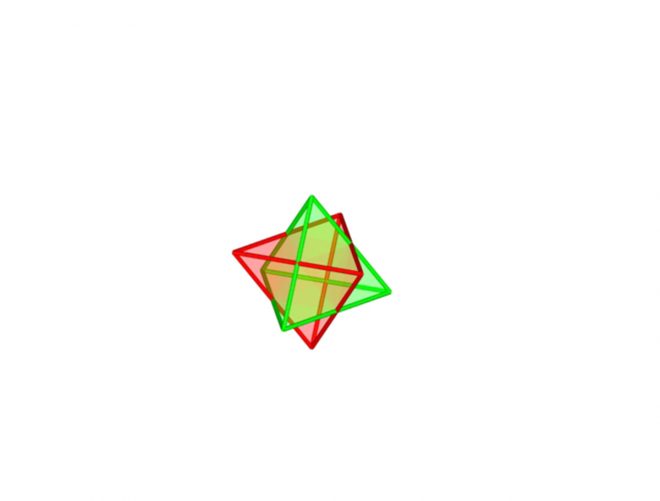
Tetraedro / Tetraedro Invertido / Octaedro / Cubo / Dodecaedro / Icosaedro: si unimos, por dentro de un tetraedro, los puntos medios de sus caras, obtendremos otro tetraedro inscrito en el primero e inverso respecto al mismo. Si ese tetraedro inscrito e inverso, se va agrandando paulatinamente, llegará un momento en que sus aristas se intercepten por sus puntos medios con los puntos medios de las aristas del tetraedro original.
Resultan de esta manera dos tetraedros iguales e invertidos, uno respecto del otro, y cuyas aristas se interceptan por sus puntos medios.
La intercepción de dos tetraedros define un octaedro regular que queda inscrito en ambos tetraedros invertidos.
En realidad, un octaedro es el espacio común o compartido por los dos tetraedros invertidos cuyas aristas se entrecruzan por sus puntos medios. Las aristas del octaedro van de punto medio a punto medio de las aristas de ambos tetraedros y sus vértices coinciden con la intercepción, por su puntos medios, de las aristas de los dos tetraedros invertidos.

Figura 1
La unión de los vértices de dos tetraedros iguales e invertidos que se interceptan por los puntos medios de sus aristas, determina un cubo o hexaedro. En ese cubo o hexaedro se encuentra, a su vez, inscrito el octaedro que habíamos definido anteriormente y lo hace de tal manera, que sus vértices tocan los puntos medios de las caras del cubo.

Figura 2
Si ese octaedro, que se inscribe en el cubo o hexaedro se va agrandando paulatinamente llegará un momento en que las aristas del cubo y del octaedro se interceptarán por su puntos medios, si se sigue agrandando el octaedro, será el cubo el que quedaría inscrito en el octaedro, de tal forma que sus vértices tocarían los puntos medios de las caras del octaedro.

Figura 3
Igualmente de la unión de los vértices resultantes de la intersección adecuada de CINCO hexaedros o cubos resultará un dodecaedro regular, en el cual quedarán inscritos todos los poliedros anteriormente definidos pudiéndose ampliar el numero de poliedros inscritos en el dodecaedro, puesto que al estar éste definido por cinco cubos, igualmente podríamos ampliar a cinco octaedros (uno por cada cubo) y a diez tetraedros en parejas invertidas, a razón, por tanto, de dos por cubo.
La intersección de los cinco cubos hay que efectuarla de tal forma que en la caras pentagonales del dodecaedro se formen estrellas de cinco puntas, estrellas pitagóricas, formadas por cinco trazos cada una y que van de vértice a vértice opuesto de las caras pentagonales regulares del dodecaedro. Cada trazo de cada una de las estrellas de cinco puntas que se inscriben en los pentágonos del dodecaedro ha de corresponderse con una arista perteneciente, cada vez, a un cubo diferente.
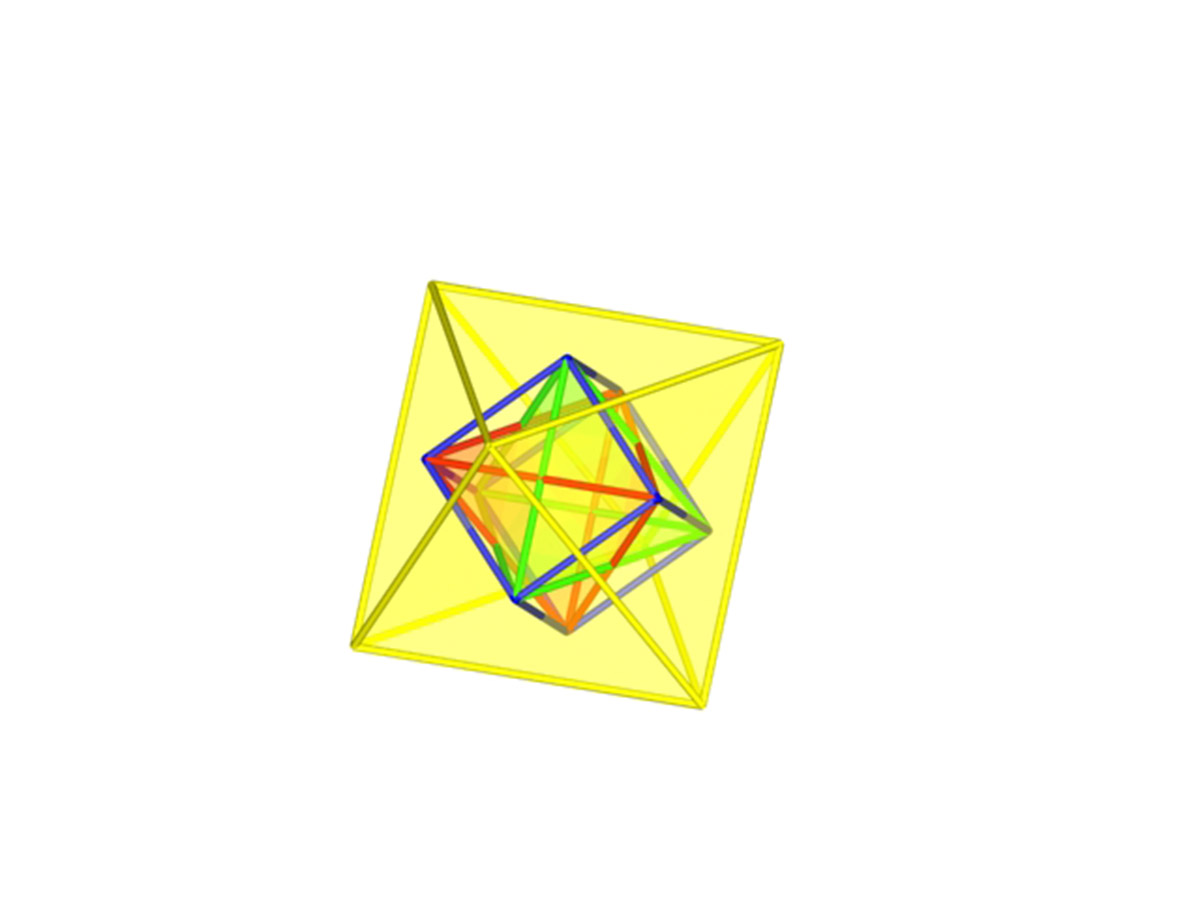
Figura 4
Si por dentro del dodecaedro unimos los centros de todas su caras pentagonales obtendremos un icosaedro regular inscrito en el dodecaedro cuyos vértices tocan los puntos medios de las caras del dodecaedro, si agrandamos paulatinamente el icosaedro, llegara un momento en que las aristas del dodecaedro e icosaedro se interceptan, por sus puntos medios, formando ángulos de 90º entre ellas. Por los puntos o zonas de intersección de las mencionadas aristas pasan los ejes cuaternarios correspondientes a los cinco cubos o hexaedros que se interceptan e inscriben en el dodecaedro, esos ejes cuaternarios no son sino los correspondientes u homólogos a los ejes de cinco sistemas clásicos de coordenadas espaciales íntimamente correlacionados.
Al igual que hemos referido anteriormente respecto de otros poliedros, hemos de advertir también que si se agranda convenientemente el icosaedro que se inscribe o intercepta, en/con, el dodecaedro, llegará un punto en que el dodecaedro quedará inscrito en el icosaedro regular, de manera que los vértices del dodecaedro tocarían los puntos medios de las acaras triangulares del icosaedro.

Figura 5
Conviene citar también que cada cara pentagonal del dodecaedro puede sustituirse por una pirámide triangular equilátera que tienen, entre sí, ángulos desiguales. Este curios poliedro se encuentra representado en este trabajo en / menú: Complejo Poliédrico Regular — CPR Simple — CPR Simple / Ejes – Secuencias 1,2 y 3. Concretamente en las Fig. s1-10, Fig. s1-11, Fig. s2-10, Fig. s2-11, Fig. s3-10 y Fig. S3-11, correspondientes a las citadas secuencias.
No voy a comentar particularmente las Fig. 1,2,3,4 y 5 de Dualidades, porque he preferido hacer una descripción ordenada y amplia que, a groso modo, coincide con una descripción general de las génesis del CPR, lo que hace innecesario comentarlas, en particular, puesto que visto lo dicho o descrito resultan perfectamente compresibles y adecuadas para entender el texto.