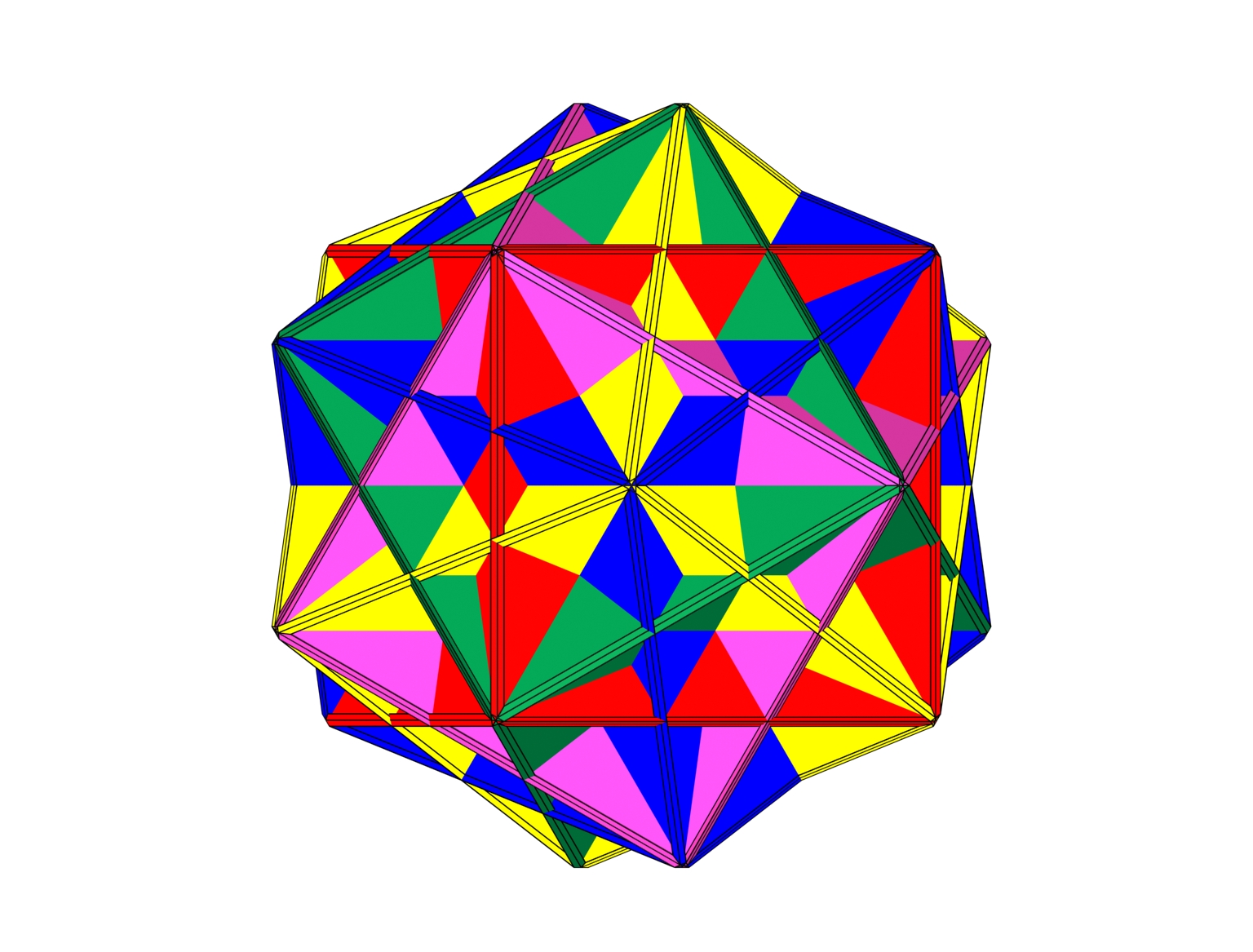
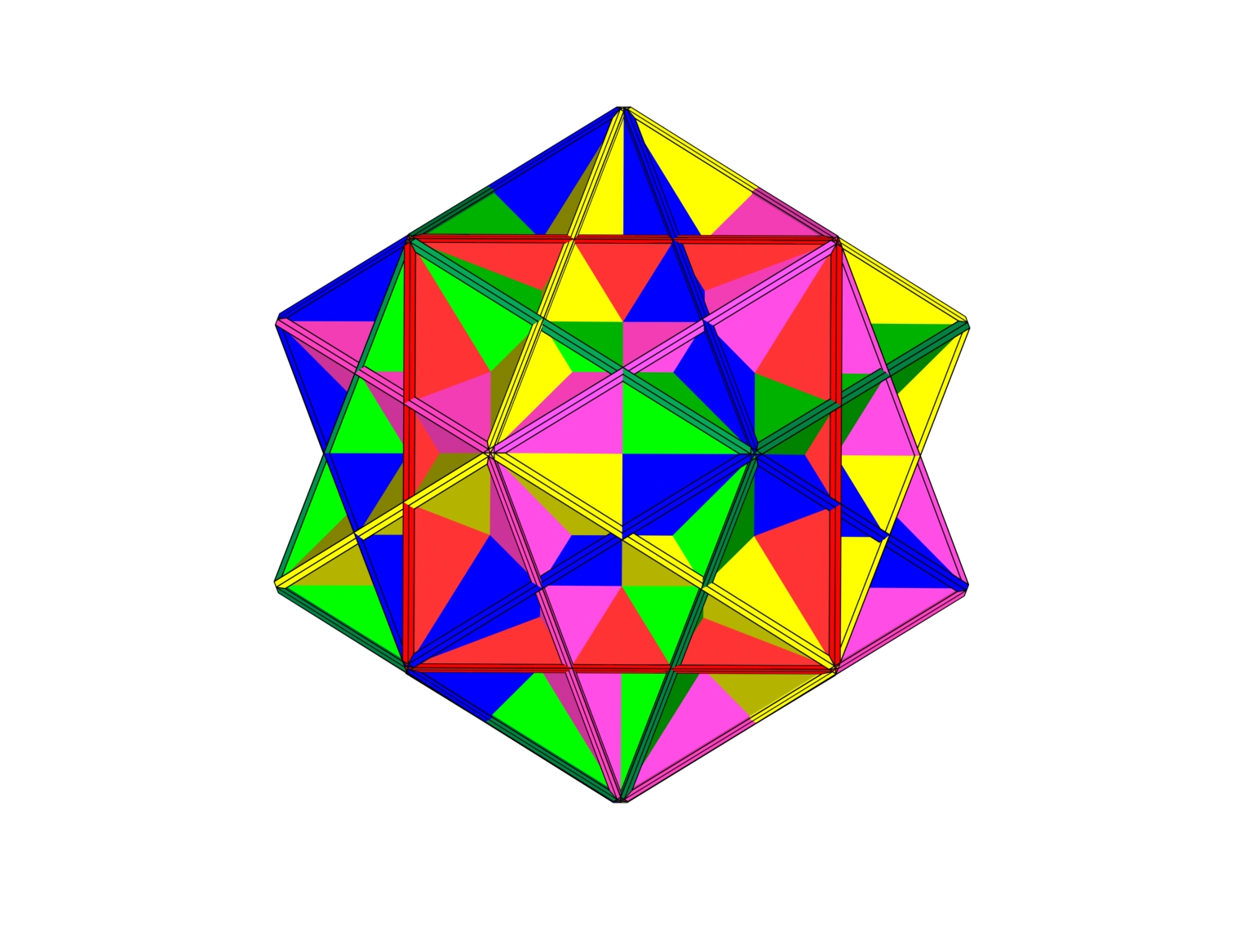
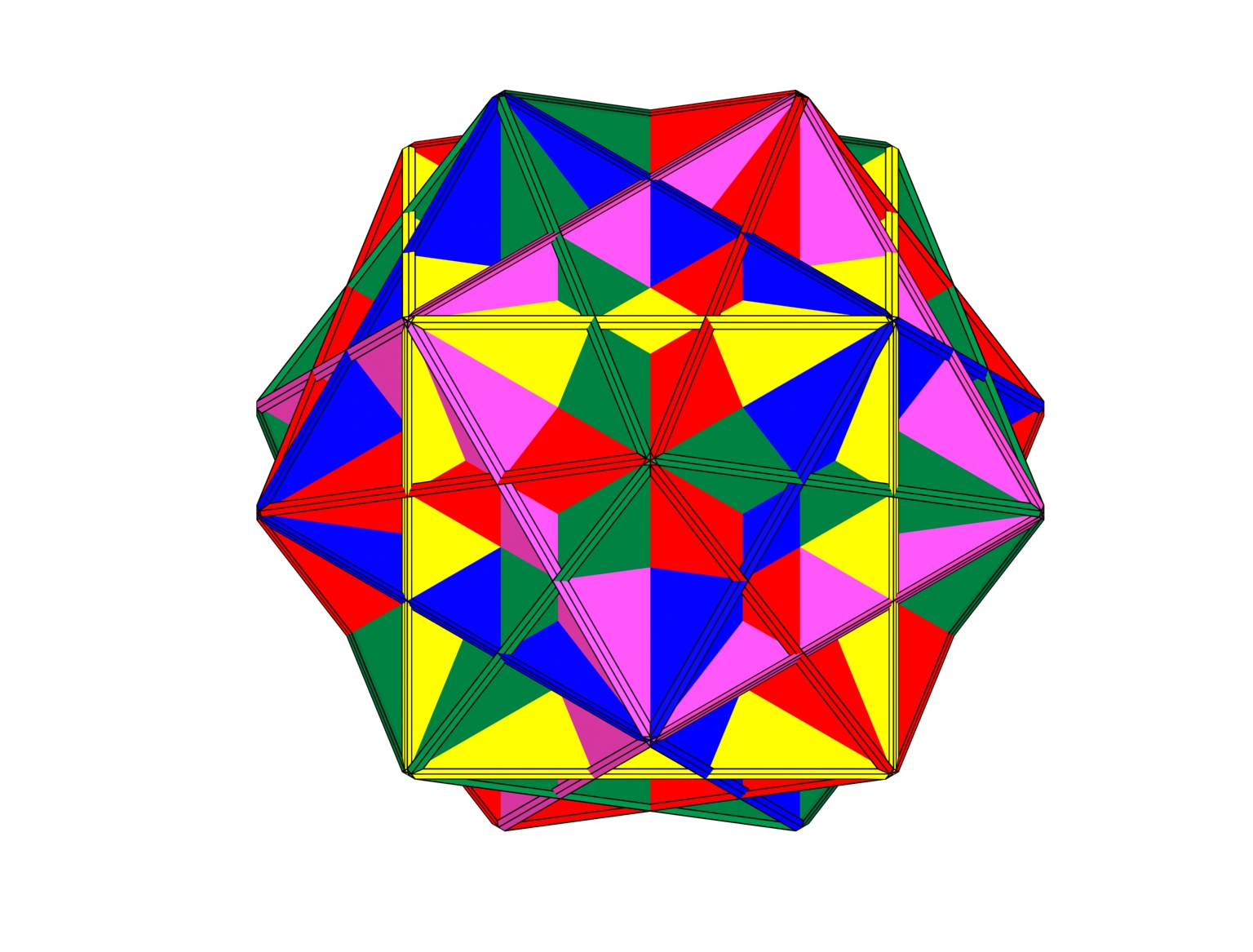
Intersección 5 Hexaedros
INTERSECCION DE 5 HEXAEDROS
Secuencia 1 Fig. 1:
Intersección de cinco hexaedros que se corresponden cada uno de ellos con la unión de los vértices de cada una de las parejas de tetraedros invertidos que estudiamos en el punto referente a la intersección de 10 tetraedros.
Además cada uno de estos hexaedros contiene o inscribe un octaedro regular cuyos vértices están situados en los puntos medios de las caras de los cubos.
Figura s1-1
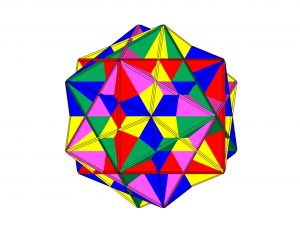
Figura s1-2
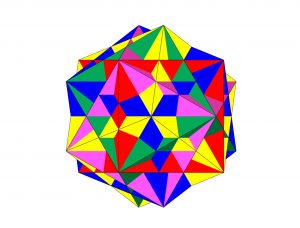
Figura s1-3
Poco a poco, vamos encontrando sentido al Complejo Poliédrico que nos ocupa y que es objeto de nuestro estudio, hemos visto como la intersección de 10 tetraedros determinaba o definía la existencia de 5 octaedros y 5 cubos, a su vez, estos octaedros y cubos también interceptaban entre ellos y compartían estructuras comunes (ej. vértices, caras con vértices, etc.), veremos como de la unión de los vértices que se generan con la intersección de los cinco cubos se define un dodecaedro regular que acabará conteniendo todos los numerosos cuerpos que hasta ahora hemos estudiado.
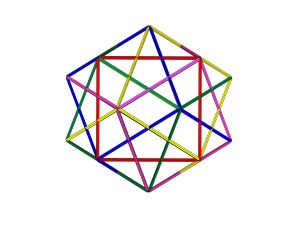
Figura s2-1
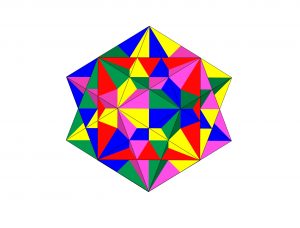
Figura s2-2
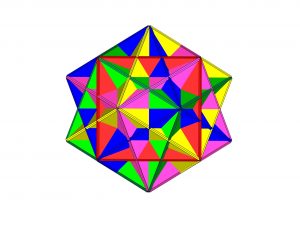
Figura s2-3
La intersección de los cinco cubos se produce de tal manera que cada arista es interceptada por otras dos, y cada uno de los veinte vértices que se generan será ocupado por aristas pertenecientes a dos y sólo a dos cubos diferentes, por otra parte, con una arista de cada cubo se generan doce estrellas pentagonales cuyos trazos son uno de cada color aisladamente consideradas y que se inscriben en las doce caras pentagonales de un dodecaedro regular, cada arista de cada color se corresponde con el trazo recto que discurre entre dos vértices opuestos de un pentágono regular.
Podemos adelantar también, que si unimos los puntos medios de las caras de un dodecaedro determinaremos un icosaedro, e igualmente si unimos los puntos medios de las caras de un icosaedro obtendremos un dodecaedro. Igualmente dodecaedro e icosaedro se interceptan a nivel de los puntos medios de sus aristas dando lugar mediante distintas actuaciones a diversos tipos de poliedros, esta última opción es la que he elegido para representar al Complejo Poliédrico Regular Complejo.
Secuencia 1 Fig. 2:
Intersección de cinco cubos de caras planas.
Secuencia 1 Fig. 3:
Intersección de cinco hexaedros de caras planas y aristas prismático triangulares regulares.
En cuanto al resto de las figuras correspondientes a las secuencias 2 y 3 se corresponden con distintas perspectivas espaciales de anteriormente estudiado.
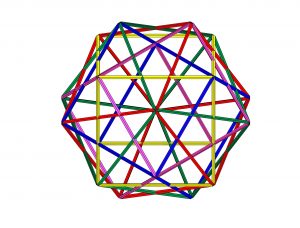
Figura s3-1
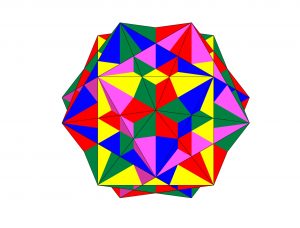
Figura s3-2
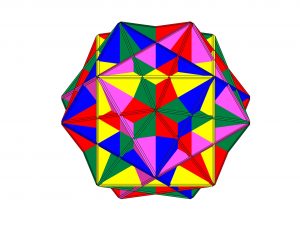
Figura s3-3